Es una correspondencia entre dos conjuntos de elementos. El primer conjunto de elementos se llama dominio y el segundo rango.
Una relación  , de los conjuntos
, de los conjuntos 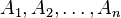 es un subconjunto del producto cartesiano
es un subconjunto del producto cartesiano
 , de los conjuntos
, de los conjuntos 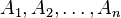 es un subconjunto del producto cartesiano
es un subconjunto del producto cartesiano
- Una relación binaria es una relación entre dos conjuntos.El concepto de relación implica la idea de enumeración de algunos de los elementos, de los conjuntos que forman tupas.Un caso particular es cuando todos los conjuntos de la relación son iguales:
 en este caso se representa
en este caso se representa  como
como  , pudiéndose decir que la relación pertenece a A a la n.FUNCION:Es una relación donde a cada valor del primer conjunto, le corresponde un sólo valor del segundo conjunto.
, pudiéndose decir que la relación pertenece a A a la n.FUNCION:Es una relación donde a cada valor del primer conjunto, le corresponde un sólo valor del segundo conjunto.
Por ejemplo el área A de un círculo es función de su radio r: el valor del área es proporcional al cuadrado del radio, A = π·r2. Del mismo modo, la duración T de un viaje de tren entre dos ciudades separadas por una distancia d de 150 km depende de la velocidad v a la que este se desplace: la duración es inversamente proporcional a la velocidad, T = d / v. A la primera magnitud (el área, la duración) se la denomina variable dependiente, y la cantidad de la que depende (el radio, la velocidad) es la variable independiente.


No hay comentarios:
Publicar un comentario