Asintotas de La Gráfica de Una Función Racional

 Si la distancia de una recta a una gráfica tiende a cero ( la recta se aproxima a la gráfica, casi hasta rozarla ) cuando un punto está se aleja del origen, entonces la recta es una asíntota de la gráfica.

       Pasos para trazar la gráfica de una función racional.

 Supongamos que  f( x) =  g( x), donde g ( x) y h ( x) son polinomios que no tienen factor común.

                                                  h( x)

1.       Encontrar los puntos de intersección con el eje x, es decir, los ceros reales del numerador g( x) y localizar los puntos correspondientes sobre el eje.

2.       2. Hallar los ceros reales del denominador  h( x ). Para cada cero real trace la asíntota vertical x= a con una línea punteada.

3.        Ubicar el punto de intersección f ( o ) con el ejey, si existe, localizar el punto  ( o,f ( o) en el eje y).

4.       Determinar, en caso de que las haya, la discontinuidad removible.

5.       Hallar  al menos dos puntos de la gráfica que estén a la derecha de la asíntota vertical y a la izquierda de la misma, en caso de que los haya.

6.       Aplicar  el teorema sobre asíntotas horizontales.

7.        Unir, mediante curvas, los puntos obtenidos para trazar la gráfica de la función.

Raices De la Funcion Racional

Existe  una estrecha relación entre las raíces de una función racional y las de un polinomio: su numerador ( recuerda  que para que una fracción sea cero, basta  con que el numerador tenga ese valor )

Las raíces de una función racional corresponden a las raíces del polinomio que  aparece en e  numerador. Se determina resolviendo la ecuación que resulta de igualar  ésta en cero.

Al trazar la gráfica  de una función  racional f, es importante responder estas dos preguntas

1.- ¿Qué  puede decirse de los valores de la función f( x) cuando x es cali ( pero no igual ) un cero del denominador?

2.- ¿ Que  se puede decir de los valores de la función f ( x) cuando x es grande positiva  o x grande negativa?

FUNCION RACIONAL

Una función racional es aquella de la forma  f( x) = P( x),  donde  p( x) y Q ( x ) son polinomios y  Q ( x)  es diferente de cero, por ejemplo :                                   Q( x)¹

a)      F( x) = 4x-3                     f( x)=  8                                                c) f8 x)= x -  4______

                         X²-4                                    x                                                    x²-7x + 12

El dominio de definición de una función racional es el conjunto de todos los números reales, excepto aquellos que anulan su denominador.

Para la construcción del dominio de una función racional se consideran, en primera instancia, todos los números reales. De ellos se suprimen los valores que vuelven cero al denominador

Ejemplo

     En la función f (x) = ^x2+6x + 5,  para  conocer el valor de x que hace cero al denominador, resolvemos

                                              x-4

x-4= 0, encontrando x= 4. Por lo tanto, el dominio es { x E R| x≠4},  es decir todo R excepto  x= 4 ó Dom  f( x) = R-{ 4 } siendo  la función discontinua.

Teoremas

Teorema de la factorización  Lineal:    cualquier polinomio cuyo grado  n esté definido, tendrá exactamente n factores lineales.

Ejemplo:

 X+ 1,  es un polinomio de grado 1 por lo tanto tiene una raíz.

X² +5x+ 6,es un polinomio de grado 2 así que tiene dos raíces.

X³ +3,5x² + 3.5x + 1, es un polinomio de tercer grado y tiene tres raíces, x⁴  - 4, cuatro raíces.

Prueba  del cero racional.  Para un polinomio f( x )  = a_n xⁿ + a_n-1 x^n-1 + a_n-2 x^n-2 + …+ a₁ x +a₀  los ceros  son de la

forma   factor  de a₀    si a_n ≠ 0 y los coeficientes son enteros.

              Factor de  a_n

Ejemplo:

Para la función f( x ) = x³ + 9x² + 26 x + 24; a_o = 24  y  a_n= 1

24  = 1, 2, 3, 4, 6, 8, 12, 24, = ± 1, ± 2, ± 3, ± 4, ± 6, ± 8, ± 12, ±24;  son todos los divisores que, posiblemente sean ceros reales en el polinomio.

 Teorema fundamental del algebra.  Todo polinomio de grado n tiene exactamente  n raíces,  que pueden ser de tres tipos: simples, múltiples  o complejas.

Ejemplos :

f ( x ) = x + 24 y g ( x ) = 2x – 4 son polinomios de raíz simple.

h( x ) = x² + 4x + 4 I ( x ) = x³ – 3x²+ 3x + 1, son polinomios de multiplicidad 2 y 3 ( la raíz está duplicada  y triplicada  respectivamente  ).

                                     

    S ( x ) = x³ – 3x²  +  4x – 12 y T ( x ) = x³ + 4x  son  polinomios de raíces  complejas.

  Gráfica de funciones polinomiales: Los ceros reales representan los puntos de intersección de un polinomio con el eje x, a partir de ahí es posible establecer la curva de un polinomio, Un valor  anterior al cero real mas pequeño, substituyéndola en la función nos permite conocer si la curva es creciente o decreciente, dependiendo  si la pendiente de la curva es positiva o negativa, respectivamente.

Division Sintetica

Ahora, podemos definir lo siguiente.

Función polinomial.  Si una  función f está definida por  f(x)=a_nxⁿ+a_n-2x^­2+a₁x+a₀

donde a_0, a_1,…,a_n son números  reales a_n ≠0 y n≥ 0 se llama función polinomial

Son ejemplos de polinomios : S ( x) =x^{2 +}20x que es un binomio, t ( x) = x²+20x+100 que es un trinomio y w ( x) =x⁶+ 20x³+32x²+ 16 que es un polinomio de cuatro términos.

Cero reales.  Son las raíces que hacen cero a un polinomio, y en una gráfica cortan al eje x.

Cero complejos.  Tienen una parte real  y una parte imaginaria, son binomios conjugados y en una gráfica no cortan al eje x.

 Ejemplo:

 Las raíces  reales x=5, x=2, y x= -2 pertenecen al polinomio

F(x)= x^{3  -} 5x² – 4x + 20 y las raíces  x⁼5, x⁼2i, y x=-2i pertenecen al polinomio

g(z) =x³ -5x² +4x-20 donde el primer valor a₁ es real y los dos siguientes  son imaginarios. Los valores reales de una curva cortan al eje x del sistema cartesiano rectangular  y los valores imaginarios  nunca cortan al eje x.

Teorema del residuo,  Si r es cualquier número real el residuo de la división del polinomio P ( x )=

a₀ xⁿ +a₁x^n-1 +…+a_n x⁰   entre  x-r, es igual a P ( r). Es decir, si un polinomio f(x), se divide por  x-r, donde r es una constante, el residuo es igual al valor del polinomio cuando x= r.

Ejemplo

 Si dividimos f( x)= 2x³ +3x² – x- 4 por ( x-4), entonces el residuo será:

     f( 4 )= 128 + 48 -4 – 4= 168.

El teorema del residuo es muy útil cuando se quieren encontrar los factores de un polinomio.

Para x= 1, f( 1)= 2+3-1-4= 0, por lo tanto ( x-1) es  un factor.

Teorema del factor.  Si el residuo de la división de un polinomio es cero, entonces  x – r es factor  del polinomio, r su raíz y viceversa; f ( r) = 0.

                     Ejemplo

                                                                                                                          

            Si f(x)= x² + x – 6, los factores son x-2 y x+ 3 porque

               F( 2)= (2)² + (2)- 6=0 y f ( -3 ) = ( -3)² + ( - 3) – 6 = 0.

                                                                                                                          

  El teorema  del factor se deduce del teorema del residuo.

División  sintética.  Es el método  de división de polinomios que usa los teoremas  del residuo y del factor para conocer  sus cocientes. Ejemplo, dividir  h ( x ) = x² +x- 6 entre  x – 2 da como cociente  x + 3.

  Es importante  que te familiarices con el uso de la división sintética. Para tener mayor afectividad se recomiendan los pasos siguientes:

a)    Ordena los coeficientes del polinomio y lista  los coeficientes en forma descendente.      

b)    Si faltan términos  en el polinomio descendente, escribe coeficientes ceros en sus posiciones.

c)    Para dividir  el polinomio entre  x - a, coloca a la derecha con signo positivo y, para el divisor x ⁺a, utiliza  - a.

d)    Baja  el primer coeficiente del polinomio dividendo.

e)    Multiplicar por a y reduce  la suma para cada  columna  y realiza consecutivamente por el pasto anterior.

f)      Especifica  el polinomio cociente y residuo obtenido.

La división  sintética se usa solamente para dividir  un polinomio entre un binomio  de la forma x-a, donde a  es una constante. Si el factor lineal propuesto es x-4, para la división sintética se toma entonces  x=4. Si el factor  es, x⁺² el valor utilizado será x=-2.

MÉTODO DE SOLUCIÓN DE LAS ECUACIONES FACTORIZABLES ASOCIADAS A UNA FUNCIÓN POLINOMIAL DE GRADOS TRES Y CUATRO

Para   poder graficar una función de grado tres o de grado cuatro, lo primero que hay que decidir es el intervalo a elegir donde se encuentren los cambios más significativos, para ello es recomendable calcular las raíces, utilizando los métodos: despeje, factorización y uso de la división sintética. Conociendo los  ceros, tenemos una buena referencia para aproximar el trazo de la gráfica

   Para observar  los diferentes métodos, observaremos los ejemplos siguientes:

Ejemplo: Grafica la función f( x) = 3x³ +24

Solución:

 Para graficar, primero encontramos las raíces, hay que hacer que  y⁼0

Usaremos, en este caso, el despeje:

3x³+24=0

3x³=  - 24

x³ =  - 24

           3

x³ = -8

x^{3=  3√ -8}

X=-2

La función tiene una sola raíz: x=-2 ( de la multiplicidad 3) sí que para escoger el intervalo adecuado debemos incluir  la raíz y la intersección con el eje vertical f(o)= 3 ( 0 ) 3+3+24 =24, por lo tanto el intervalo que sugerimos para la gráfica  es [-3, 1]:  

Tipos de Relaciones

Relación unaria: un solo conjunto 

Relación binaria: con dos conjuntos 

Relación terciaria: con tres conjuntos 

Relación cuaternaria: con cuatro conjuntos 

...

Relación n-ria: caso general con n conjuntos 

Relación y Función

Relación:
Es una correspondencia entre dos conjuntos de elementos. El primer conjunto de elementos se llama dominio y el segundo rango.

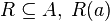
Una relación , de los conjuntos 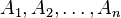 es un subconjunto del producto cartesiano

Una relación binaria es una relación entre dos conjuntos.

El concepto de relación implica la idea de enumeración de algunos de los elementos, de los conjuntos que forman tupas.

Un caso particular es cuando todos los conjuntos de la relación son iguales:  en este caso se representa  como , pudiéndose decir que la relación pertenece a A a la n.

FUNCION:

Es  una relación donde a cada valor del primer conjunto, le corresponde un sólo valor del segundo conjunto.

Por ejemplo el área A de un círculo es función de su radio r: el valor del área es proporcional al cuadrado del radio, A = π·r². Del mismo modo, la duración T de un viaje de tren entre dos ciudades separadas por una distancia d de 150 km depende de la velocidad v a la que este se desplace: la duración es inversamente proporcional a la velocidad, T = d / v. A la primera magnitud (el área, la duración) se la denomina variable dependiente, y la cantidad de la que depende (el radio, la velocidad) es la variable independiente.